Research Statement

Vision Physical simulation is a powerful tool for analysis and design, but current methods require tedious parameter tuning to get feasible results. This is impractical for tasks such as inverse design and reinforcement learning which require thousands of simulations. My research goal is to enable the use of simulation as a tool that requires minimal to no parameter tuning, effectively lowering the barrier of entry to using simulation.

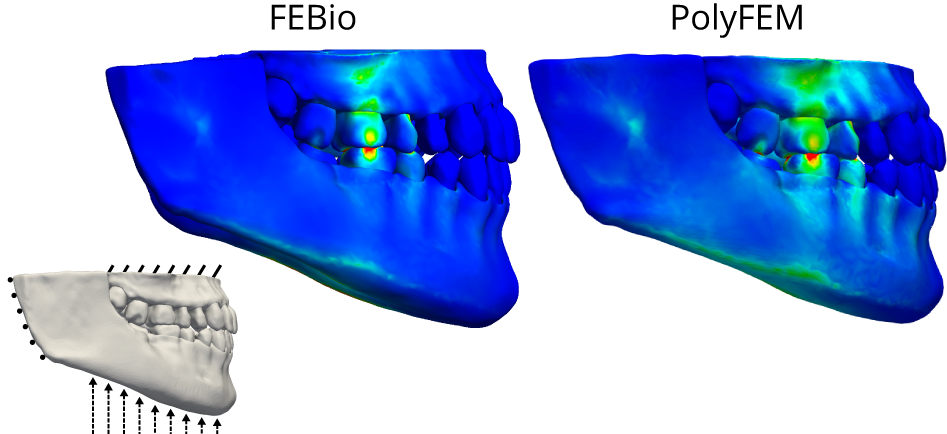
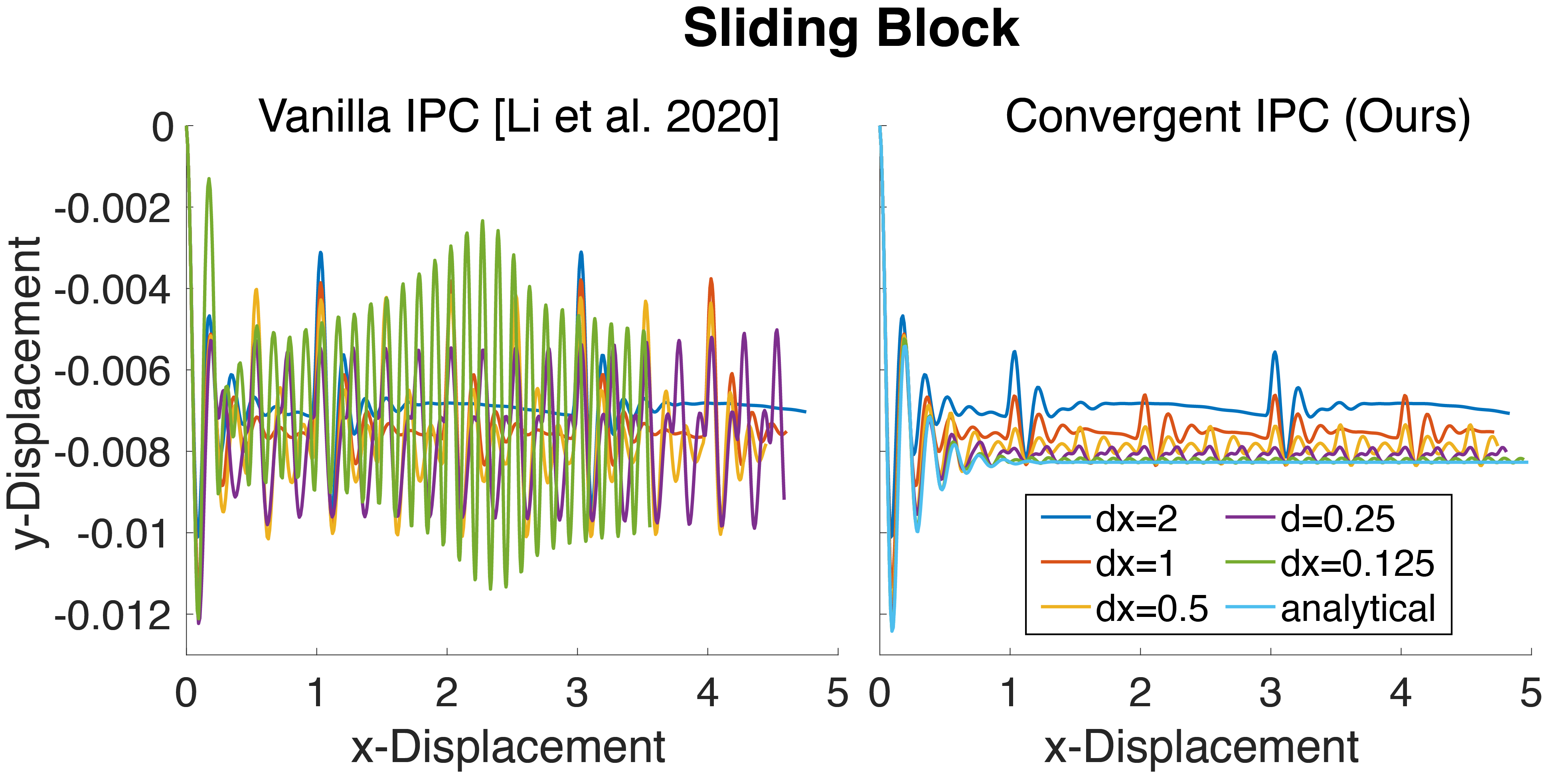
Approach My research focuses on (open-source) accurate simulation methods with parameter-free robustness guarantees. Namely, we introduce the first set of algorithms for contact simulation that are unconditionally robust, require minimal parameter tuning, and are fully differentiable (capable of inverse design). Matching experimental data in one shot is finally an achievable goal.

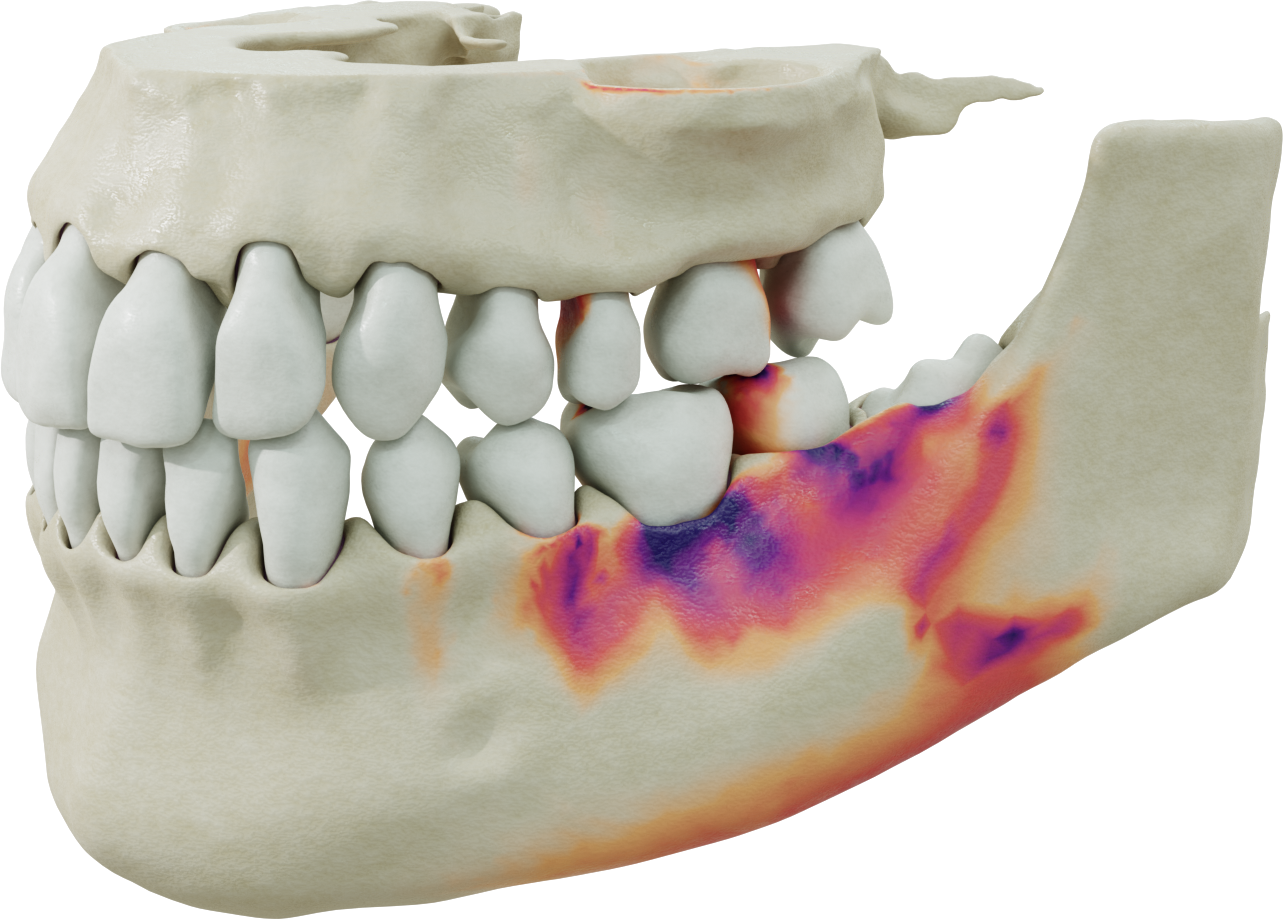
Impact The widespread use of simulation amplifies the impact of my research. My contributions have pushed the boundaries of knowledge in multiple fields, including physically-based animation, automated design, robotics, and biomechanics. By pioneering unconditionally robust, accurate, and fully differentiable algorithms for contact simulation, I have democratized simulation, making it a more accessible and powerful tool for design and analysis.

Thesis

Provably Robust and Accurate Methods for Rigid and Deformable Simulation with Contact
Zachary Ferguson
Ph.D. Dissertation, New York University, 2023
Summary: In this thesis, we introduce Incremental Potential Contact (IPC), the first simulation algorithm for deformable and rigid bodies that is efficient, accurate, and unconditionally robust. To verify these claims, we evaluate the efficiency and correctness of Continuous Collision Detection (CCD) algorithms and introduce the first provably correct and efficient algorithm. For improved accuracy and efficiency, we extend IPC to curved meshes and high-order bases and introduce the first physically-based adaptive meshing strategy.
Thesis

Publications

Differentiable Solver for Time-Dependent Deformation Problems with Contact
Zizhou Huang*, Davi Colli Tozoni*, Arvi Gjoka, Zachary Ferguson, Teseo Schneider, Daniele Panozzo, Denis Zorin (*Joint first authors)
ACM Transactions on Graphics, 2024 (presented at SIGGRAPH 2024)
Summary: We introduce a general differentiable solver for both static and dynamic deformation problems with frictional contact. We support differentiation with respect to all physical parameters involved (e.g., shape, material parameters, friction parameters, and initial conditions). We accomplish this by leveraging the Incremental Potential Contact formulation to solve PDE-constrained optimization problems on scenes with complex geometries.
Project Page Paper Video Code
A Systematic Comparison Between FEBio and PolyFEM for Biomechanical Systems
Liam Martin, Pranav Jain, Zachary Ferguson, Torkan Gholamalizadeh, Faezeh Moshfeghifar, Kenny Erleben, Daniele Panozzo, Steven Abramowitch, Teseo Schneider
Computer Methods and Programs in Biomedicine, 2024
Summary: We validate PolyFEM's (including Incremental Potential Contact) capabilities towards simulating biomechanical systems by comparing it against the well-established finite element solver, FEBio.
Paper
In-Timestep Remeshing for Contacting Elastodynamics
Zachary Ferguson, Teseo Schneider, Danny M. Kaufman†, Daniele Panozzo† (†Joint last authors)
ACM Transactions on Graphics (SIGGRAPH), 2023
Summary: We propose a fully coupled, adaptive meshing algorithm for contacting elastodynamics where remeshing steps are tightly integrated, implicitly, within the time-step solve. Our algorithm refines and coarsens the domain automatically by measuring physical energy changes within each ongoing time-step solve while guaranteeing invariants (maintaining intersection- and inversion-free trajectories) are preserved.
Project Page Paper Video Code Data
High-Order Incremental Potential Contact for Elastodynamic Simulation on Curved Meshes
Zachary Ferguson, Pranav Jain, Denis Zorin, Teseo Schneider, Daniele Panozzo
ACM SIGGRAPH 2023 Conference Proceedings
Summary: We extend the Incremental Potential Contact method to high-order finite element basis and curved meshes. We do so by coupling together a high-order volumetric representation with a linear surface representation. This provides improved accuracy while maintaining efficient collision detection and response, leading to significant improvements in running times.
Project Page Paper Video Code Data
LibHip: An open-access hip joint model repository suitable for finite element method simulation
Faezeh Moshfeghifar, Torkan Gholamalizadeh, Zachary Ferguson, Teseo Schneider, Michael Bachmann Nielsen, Daniele Panozzo, Sune Darkner, Kenny Erleben
Computer Methods and Programs in Biomedicine, 2022
Summary: Population-based finite element analysis of hip joints allows us to understand the effect of inter-subject variability on simulation results. To aid in this direction, we reconstruct 11 subject-specific models from CT scans and release them as an open-access repository. We evaluate our models using both mesh quality metrics and simulation experiments.
Paper Data
Open-Full-Jaw: An open-access dataset and pipeline for finite element models of human jaw
Torkan Gholamalizadeh, Faezeh Moshfeghifar, Zachary Ferguson, Teseo Schneider, Daniele Panozzo, Sune Darkner, Masrour Makaremi, François Chan, Peter Lampel Søndergaard, Kenny Erleben
Computer Methods and Programs in Biomedicine, 2022
Summary: We share an open-access repository of 17 patient-specific computational models of human jaws and the utilized pipeline for generating them. The pipeline minimizes the required time for processing and any potential biases in the model generation process caused by human intervention.
Paper Data
A Cross-Platform Benchmark for Interval Computation Libraries
Xuan Tang, Zachary Ferguson, Teseo Schneider, Denis Zorin, Shoaib Kamil, Daniele Panozzo
International Conference on Parallel Processing and Applied Mathematics (PPAM), 2022
Summary: We introduce a benchmark for interval arithmetic computation and test it on four C/C++ libraries: filib, filib++, Boost, and BIAS. Each library is evaluated based on correctness, output interval size, speed, consistency, and portability.
Project Page Paper Code (Filib CMake)
Fast and Exact Root Parity for Continuous Collision Detection
Bolun Wang, Zachary Ferguson, Xin Jiang, Marco Attene, Daniele Panozzo, Teseo Schneider
Computer Graphics Forum (Eurographics), 2022
Summary: We introduce the first exact root parity method for continuous collision detection that is robust to degenerate configurations and is implemented directly using floating-point numbers while accounting for rounding errors.
Project Page Paper Presentation (YouTube) Presentation (Bilibili) Code
Intersection-free Rigid Body Dynamics
Zachary Ferguson, Minchen Li, Teseo Schneider, Francisca Gil-Ureta, Timothy Langlois, Chenfanfu Jiang, Denis Zorin, Danny M. Kaufman, Daniele Panozzo
ACM Transactions on Graphics (SIGGRAPH), 2021
Summary: We introduce the first algorithm for time-stepping rigid body dynamics, with contacts and friction, which guarantees intersection-free configurations at every time step. Additionally, we propose a novel collision detection algorithm for curved trajectories.
Project Page Paper Video Code
A Large Scale Benchmark and an Inclusion-Based Algorithm for Continuous Collision Detection
Bolun Wang*, Zachary Ferguson*, Teseo Schneider, Xin Jiang, Marco Attene, Daniele Panozzo (*Joint first authors)
ACM Transactions on Graphics, 2021 (presented at SIGGRAPH 2022)
Summary: We introduce a benchmark to evaluate the accuracy, correctness, and efficiency of continuous collision detection algorithms; and a fast algorithm capable of detecting all collisions using floating-point computation.
Project Page Paper Presentation Code Data
DHFSlicer: Double Height-Field Slicing For Milling Fixed Thickness Materials
Jinfan Yang, Chrystiano Araújo, Nicholas Vining, Zachary Ferguson, Enrique Rosales, Daniele Panozzo, Sylvain Lefebvre, Paolo Cignoni, Alla Sheffer
ACM Transactions on Graphics (SIGGRAPH Asia), 2020
Summary: We introduce an automatic method for the fabrication of complex geometric objects. We start by decomposing them into bounded thickness 3-axis millable slices. Each slice is then milled and assembled to form the target object.
Project Page Paper
Incremental Potential Contact: Intersection- and Inversion-free, Large-Deformation Dynamics
Minchen Li, Zachary Ferguson, Teseo Schneider, Timothy Langlois, Denis Zorin, Daniele Panozzo, Chenfanfu Jiang, Danny M. Kaufman
ACM Transactions on Graphics (SIGGRAPH), 2020
Summary: We propose Incremental Potential Contact (IPC) for robust and accurate time-stepping of nonlinear elastodynamics. IPC guarantees intersection- and inversion-free trajectories regardless of materials, time step sizes, velocities, or deformation severity.
Project Page Paper Video Code
Stitch Meshing
Kui Wu, Xifeng Gao, Zachary Ferguson, Daniele Panozzo, Cem Yuksel
ACM Transactions on Graphics (SIGGRAPH), 2018
Summary: We introduce the first fully automatic pipeline for converting arbitrary 3D models into knit structures that can be animated with yarn-level simulation and fabricated via 3D printing.
Project Page Paper Video Code
Seamless: Seam erasure and seam-aware decoupling of shape from mesh resolution
Songrun Liu*, Zachary Ferguson*, Alec Jacobson, Yotam Gingold (*Joint first authors)
ACM Transactions on Graphics (SIGGRAPH Asia), 2017
Summary: We present seam-aware mesh processing techniques that eliminate seam artifacts in textures and decimate a mesh, including its seams, while preserving its parameterization and seam-free appearance. This allows the artifact-free display of surface signals (color, normals, positions, displacements, skin weights) with the standard GPU rendering pipeline.
Project Page Paper Video Code (Seam Erasure) Code (Decimater)

Preprints

Convergent Incremental Potential Contact
Minchen Li, Zachary Ferguson, Teseo Schneider, Timothy Langlois, Denis Zorin, Daniele Panozzo, Chenfanfu Jiang, Danny M. Kaufman
arXiv, 2023
Summary: We reformulate the Incremental Potential Contact (IPC) model in the continuous setting and provide a convergent discretization. We demonstrate and analyze the convergence behavior of this new model and discretization on a range of elastostatic and dynamic contact problems, and evaluate its accuracy on both analytical benchmarks and application-driven examples.
arXiv
Time of Impact Dataset for Continuous Collision Detection and a Scalable Conservative Algorithm
David Belgrod, Bolun Wang, Zachary Ferguson, Xin Zhao, Marco Attene, Daniele Panozzo, Teseo Schneider
arXiv, 2023
Summary: We introduce a large-scale benchmark for broad- and narrow-phase continuous collision detection (CCD) with the exact time of impact. We use this benchmark to evaluate the accuracy, correctness, and efficiency of 13 state-of-the-art CCD algorithms. We further improve upon the state-of-the-art by introducing a new algorithm for CCD designed to be scalable on modern parallel architectures (CPUs and GPUs) while provably correct under floating-point arithmetic.
Project Page arXiv Video Code